VISCOSITY
SUBJECT : FLUID MECHANICS
What is Viscosity?
Viscosity is that property of a fluid by virtue of which it offers resistance to the movement of one layer of fluid over an adjacent layer. It is primarily due to cohesion and molecular momentum exchange between fluid layers, and as flow occurs, these effects appear as shearing stresses between the moving layers of fluid.
Consider two plates (Below Figure) sufficiently large (so that edge conditions may be neglected) placed a small distance Y apart, the space between them being filled with fluid. The lower plate is assumed to be at rest, while the upper one is moved parallel to it with a velocity V by the application of a force F, corresponding to area A, of the moving plate in contact with the fluid. Particles of the fluid in contact with each plate will adhere to it and if the distance Y and velocity V are not too great, the velocity v at a distance y from the lower plate will vary uniformly from zero at the lower plate which is at rest, to V at the upper moving plate. Experiments show that for a large variety of fluids
F ~ AV/Y
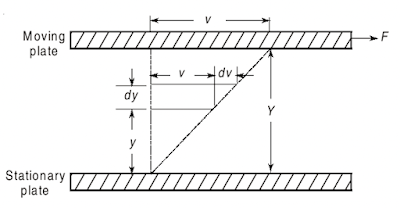 |
| Fluid motion between two planes |
It may be seen from similar triangles in Fig. 1.1 that the ratio V/Y can be replaced by the velocity gradient (dv/dy), which is the rate of angular deformation of the fluid. If a constant of proportionality µ (Greek ‘mu’) be introduced, the shear stress τ (Greek ‘tau’) equal to (F/A) between any two thin sheets of fluid may be expressed as
τ = F/A = µ.V/Y = µ.dv/dy --- Equation A
Above equation is called Newton’s equation of viscosity, and in the transposed form it serves to define the proportionality constant.
which is called the coefficient of viscosity, or the dynamic viscosity (since it involves force), or simply viscosity of the fluid. Thus the dynamic viscosity μ, may be defined as the shear stress required to produce unit rate of angular deformation. In SI units µ is expressed in N.s/m², or kg/m.s. In the metric gravitational system of units, µ is expressed in kg(f)-sec/m² or msl/m-sec. In the metric absolute system of units µ is expressed in dyne-sec/m² or gm(mass)/cm-sec which is also called ‘poise’ after Poiseuille. The ‘centipoise’ is one hundredth of a poise. In the English gravitational system of units µ is expressed in lb(f)-sec/ft² or slug/ft-sec and in the English absolute system of units it is expressed in pdl-sec/ft² or lb(m)/ft-sec. The numerical conversion from one system to another is as follows

In many problems involving viscosity there frequently appears a term dynamic viscosity µ divided by mass density ρ. The ratio of the dynamic viscosity µ and the mass density ρ is known as Kinematic viscosity and is denoted by the symbol υ (Greek ‘nu’) so that υ = μ/ρ
On analysing the dimensions of the kinematic viscosity it will be observed that it involves only the magnitudes of length and time. The name kinematic viscosity has been given to the ratio (µ/ρ) because kinematics is defined as the study of motion without regard to the cause of the motion and hence it is concerned with length and time only. In SI units υ is expressed in m2/s. In the metric system of units υ is expressed in cm2/sec or m2/ sec. The unit cm2/sec is termed as ‘stoke’ after G.G. Stokes and its one-hundredth part is called ‘centistoke’. In the English system of units it is expressed in ft2/sec. The numerical conversion from one system to another is as follows:

The dynamic viscosity µ of either a liquid or a gas is practically independent of the pressure for the range that is ordinarily encountered in practice. However, it varies widely with temperature. For gases, viscosity increases with increase in temperature while for liquids it decreases with increase in temperature. This is so because of their fundamentally different intermolecular characteristics. In liquids the viscosity is governed by the cohesive forces between the molecules of the liquid, whereas in gases the molecular activity plays a dominant role. The kinematic viscosity of liquids and of gases at a given pressure, is essentially a function of temperature.
Common fluids such as air, water, glycerine, kerosene etc., follow Equation A. There are certain fluids which, however, do not follow Newton’s law of viscosity. Accordingly fluids may be classified as Newtonian fluids and non-Newtonian fluids. In a Newtonian fluid there is a linear relation between the magnitude of shear stress and the resulting rate of deformation i.e., the constant of proportionality µ in Equation A does not change with rate of deformation. In a non-Newtonian fluid there is a non-linear relation between the magnitude of the applied shear stress and the rate of angular deformation. In the case of a plastic substance which is a non-Newtonian fluid an initial yield stress is to be exceeded to cause a continuous deformation. An ideal plastic has a definite yield stress and a constant linear relation between shear stress and the rate of angular deformation. A thixotropic substance, which is a non-Newtonian fluid, has a non-linear relationship between the shear stress and the rate of angular deformation, beyond an initial yield stress. The printer’s ink is an example of a thixotropic liquid.
 |
| Variation of Shear Stress with Velocity Gradient |
An ideal fluid is defined as that having zero viscosity or in other words shear stress is always zero regardless of the motion of the fluid. Thus an ideal fluid is represented by the horizontal axis (τ = 0) in above figure which gives a diagrammatic representation of the Newtonian, non-Newtonian, plastic, thixotropic and ideal fluids. A true elastic solid may be represented by the vertical axis of the diagram. The fluids with which engineers most often have to deal are Newtonian, that is, their viscosity is not dependent on the rate of angular deformation, and the term ‘fluid-mechanics’ generally refers only to Newtonian fluids. The study of non-Newtonian fluids is however termed as ‘rheology’.
FAQs COVERED IN THIS POST
What is Viscosity?
What is Newtonian Fluid?
What is Dynamic Viscosity?
What is an Ideal Fluid according to Viscosity?
What are the fluids with zero viscosity?
What is Rheology?
What is the variation of shear stress with velocity gradient?
RELATED POSTS








Post a Comment