SURFACE TENSION & CAPILLARITY - FLUID MECHANICS (StudyCivilEngg.com)
SURFACE TENSION AND CAPILLARITY
SUBJECT : FLUID MECHANICS
Due to molecular attraction, liquids possess certain properties such as cohesion and adhesion. Cohesion means inter-molecular attraction between molecules of the same liquid. That means it is a tendency of the liquid to remain as one assemblage of particles. Adhesion means attraction between the molecules of a liquid and the molecules of a solid boundary surface in contact with the liquid. The property of cohesion enables a liquid to resist tensile stress, while adhesion enables it to stick to another body.
Surface tension is due to cohesion between liquid particles at the surface, whereas capillarity is due to both cohesion and adhesion.
Surface Tension
A liquid molecule on the interior of the liquid body has other molecules on all sides of it, so that the forces of attraction are in equilibrium and the molecule is equally attracted on all the sides, as a molecule at point A shown in below figure. On the other hand a liquid molecule at the surface of the liquid, (i.e., at the interface between a liquid and a gas) as at point B, does not have any liquid molecule above it, and consequently there is a net downward force on the molecule due to the attraction of the molecules below it. This force on the molecules at the liquid surface, is normal to the liquid surface. Apparently owing to the attraction of liquid molecules below the surface, a film or a special layer seems to form on the liquid at the surface, which is in tension and small loads can be supported over it. For example, a small needle placed gently upon the water surface will not sink but will be supported by the tension at the water surface.
The property of the liquid surface film to exert a tension is called the surface tension. It is denoted by σ (Greek ‘sigma’) and it is the force required to maintain unit length of the film in equilibrium. In SI units surface tension is expressed in N/m. In the metric gravitational system of units it is expressed in kg(f)/cm or kg(f)/m. In the English gravitational system of units it is expressed in lb(f)/in. or lb(f)/ft.
As surface tension is directly dependent upon inter-molecular cohesive forces, its magnitude for all liquids decreases as the temperature rises. It is also dependent on the fluid in contact with the liquid surface; thus surface tensions are usually quoted in contact with air. The surface tension of water in contact with air varies from 0.0736 N/m [or 0.0075 kg (f)/m] at 19°C to 0.0589 N/m [or 0.006 kg (f)/m] at 100°C. More organic liquids have values of surface tension between 0.0206 N/m [or 0.0021 kg (f)/m] and 0.0304 N/m [or 0.0031 kg (f)/m] and mercury has a value of about 0.4944 N/m [or 0.0504 kg(f)/m], at normal temperature and the liquid in each case being in contact with air.
The effect of surface tension is illustrated in the case of a droplet as well as a liquid jet. When a droplet is separated initially from the surface of the main body of liquid, then due to surface tension there is a net inward force exerted over the entire surface of the droplet which causes the surface of the droplet to contract from all the sides and results in increasing the internal pressure within the droplet. The contraction of the droplet continues till the inward force due to surface tension is in balance with the internal pressure and the droplet forms into sphere which is the shape for minimum surface area. The internal pressure within a jet of liquid is also increased due to surface tension. The internal pressure intensity within a droplet and a jet of liquid in excess of the outside pressure intensity may be determined by the expressions derived below.
Pressure intensity inside a droplet
Consider a spherical droplet of radius r having internal pressure intensity p in excess of the outside pressure intensity. If the droplet is cut into two halves, then the forces acting on one half will be those due to pressure intensity p on the projected area (πr²) and the tensile force due to surface tension σ acting around the circumference (2πr). These two forces will be equal and opposite for equilibrium and hence we have
p(πr²) = σ(2πr) (or) p = 2σ/r ---Equation A
Above Equation A indicates that the internal pressure intensity increases with the decrease in the size of droplet.
Pressure intensity inside a soap bubble
A spherical soap bubble has two surfaces in contact with air, one inside and the other outside, each one of which contributes the same amount of tensile force due to surface tension. As such on a hemispherical section of a soap bubble of radius r the tensile force due to surface tension is equal to 2σ(2πr). However, the pressure force acting on the hemispherical section of the soap bubble is same as in the case of a droplet and it is equal to p (πr²). Thus equating these two forces for equilibrium, we have
p(πr²) = 2σ(2πr) (or) p = 4σ/r ---Equation B
Pressure intensity inside a liquid jet
Consider a jet of liquid of radius r, length l and having internal pressure intensity p in excess of the outside pressure intensity. If the jet is cut into two halves, then the forces acting on one half will be those due to pressure intensity p on the projected area (2rl) and the tensile force due to surface tension σ acting along the two sides (2l). These two forces will be equal and opposite for equilibrium and hence we have
p(2rl) = σ(2l) (or) p = σ/r ----Equation C
Capillarity
If molecules of certain liquid possess, relatively, greater affinity for solid molecules, or in other words the liquid has greater adhesion than cohesion, then it will wet a solid surface with which it is in contact and will tend to rise at the point of contact, with the result that the liquid surface is concave upward and the angle of contact θ is less than 90° as shown in below figure (Capillarity in circular glass tubes) For example, if a glass tube of small diameter is partially immersed in water, the water will wet the surface of the tube and it will rise in the tube to some height, above the normal water surface, with the angle of contact θ, being zero. The wetting of solid boundary by liquid results in creating decrease of pressure within the liquid, and hence the rise in the liquid surface takes place, so that the pressure within the column at the elevation of the surrounding liquid surface is the same as the pressure at this elevation outside the column.
On the other hand, if for any liquid there is less attraction for solid molecule or in other words the cohesion predominates, then the liquid will not wet the solid surface and the liquid surface will be depressed at the point of contact, with the result that the liquid surface is concave downward and the angle of contact θ is greater than 90° as shown in below figure (Capillarity in circular glass tubes). For instance if the same glass tube is now inserted in mercury, since mercury does not wet the solid boundary in contact with it, the level of mercury inside the tube will be lower than the adjacent mercury level, with the angle of contact θ equal to about 130°. The tendency of the liquids which do not adhere to the solid surface, results in creating an increase of pressure across the liquid surface, (as in the case of a drop of liquid). It is because of the increased internal pressure, the elevation of the meniscus (curved liquid surface) in the tube is lowered to the level where the pressure is the same as that in the surrounding liquid.
Such a phenomenon of rise or fall of liquid surface relative to the adjacent general level of liquid is known as capillarity. Accordingly the rise of liquid surface is designated as capillary rise and the lowering of liquid surface as capillary depression, and it is expressed in terms of m or mm of liquid in SI units, in terms of cm or mm of liquid in the metric system of units and in terms of inch or ft of liquid in the English system of units.
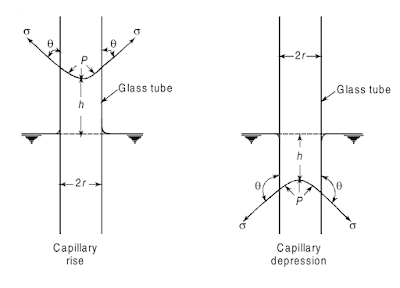 |
| Capillarity in circular glass tube |
The capillary rise (or depression) can be determined by considering the conditions of equilibrium in a circular tube of small diameter inserted in a liquid. It is supposed that the level of liquid has risen (or fallen) by h above (or below) the general liquid surface when a tube of radius r is inserted in the liquid, see above figure (Capillarity in circular glass tubes). For the equilibrium of vertical forces acting on the mass of liquid lying above (or below) the general liquid level, the weight of liquid column h (or the total internal pressure in the case of capillary depression) must be balanced by the force, at surface of the liquid, due to surface tension σ. Thus equating these two forces we have
swπr2h = 2πrσ.cosθ
where w is the specific weight of water, s is specific gravity of liquid, and θ is the contact angle between the liquid and the tube. The expression for h the capillary rise (or depression) then becomes
h = 2σ cosθ/swr --- Equation A
As stated earlier, the contact angle θ for water and glass is equal to zero. Thus the value of cosθ is equal to unity and hence h is given by the expression
h = 2σ/wr --- Equation B
Above Equation B is for capillary rise (or depression) indicates that the smaller the radius r the greater is the capillary rise (or depression)
The above obtained expression for the capillary rise (or depression) is based on the assumption that the meniscus or the curved liquid surface is a section of a sphere. This is, however, true only in case of the tubes of small diameters (r < 2.5 mm) and as the size of the tube becomes larger, the meniscus becomes less spherical and also gravitational forces become more appreciable. Hence such simplified solution for computing the capillary rise (or depression) is possible only for the tubes of small diameters. However, with increasing diameter of tube, the capillary rise (or depression) becomes much less. It has been observed that for tubes of diameters 6 mm or more the capillary rise (or depression) is negligible. Hence in order to avoid a correction for the effects of capillarity in manometers, used for measuring pressures, a tube of diameter 6 mm or more should be used.
Another assumption made in deriving Equation A is that the liquids and tube surfaces are extremely clean. In practice, however, such cleanliness is virtually never encountered and h will be found to be considerably smaller than that given by Equation A. In respect of this, Equation A will provide a conservative estimate of capillary rise (or depression).
h = 2σ.Cosθ/rw(s1-s2) ---- Equation C
in which σ is the surface tension of mercury in contact with the liquid and rest of the notation are same as defined earlier. Further if two vertical parallel plates t distance apart and each of width l are held partially immersed in a liquid of surface tension σ and sp. gr. s, then the capillary rise (or depression) h may be determined by equating the weight of the liquid column h (or the total internal pressure in the case of capillary depression) (swhlt) to the force due to surface tension (2σl cos θ). Thus we have
swhlt = 2σl cosθ (or) h = 2σcosθ/swt. ---- Equation D
FAQs COVERED IN THIS POST
What is Surface tension?
What is surface tension of fluid?
What is surface tension of a liquid molecule?
What is cohesion?
What is Adhesion?
What is Pressure Intensity inside a droplet?
What is Pressure Intensity inside a soap bubble?
What is Pressure Intensity inside a liquid jet?
What is Capillarity?
What is Capillarity of fluid?
What is Capillary rise?
What is depression in fluid mechanics?





Post a Comment